Testing Of Sequential Circuits Using Verilog

Testing is the major challenge for any VLSI design either analog or digital. And it’s something which cannot be ignored or compromised with. Before your design gets converted to a product you must be very sure about the types of problems which may occur before hand. Just think of a scenario where I have my design which performs ALU operations and we will assume that we have made this design a product without testing it. Though the simulation version of the design may work well it’s not completely enough to declare the design as fault free. There can be N number of hardware faults which may occur within the circuit and following which your design may not work as per your expectation. For digital circuits hardware testing of your design can be done with FPGA based platforms (Spartan, vertex, etc). But the question is, are you sure that the FPGA implemented design will assure fault free designs after you plan to make your product? The answers is no. FPGA may give you the hardware platform to check your design functionality but when you want to convert this design of yours into a real circuit it may have some physical faults(strictly speaking about integrated circuits).

We will now try and establish an indirect means by which we can test any sequential circuit by making some modification to our design.This example below will help you understand the work better.

                                                          FIGURE 1

The circuit above is a simple sequential circuit and the gate (circled) has to be tested now. And as you can notice that we cant directly apply inputs to this gate because its not directly connected to the primary inputs. And you can notice that the FF are converted to Scan cells which were previously D-FF. The figure below shows how a D-FF can be converted to a Scan cell which will help us to test any Gate within the circuit which are not directly accessible.  

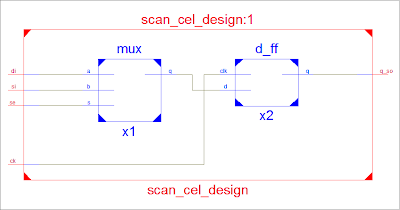
So to test any sequential circuits we have to replace all the D-FF to scan cell as shown in the figure.

Scan Cell Design:  It can operate in 2 modes 

1. Normal mode where the SE(scan enable signal) is LOW and circuit and input is read from primary inputs
2. Test mode where SE is high and can use this mode to test the internal gates and input is read from SI(scan inputs)

When SE is HIGH all the Scan Cells in the design are connected in series and when this connection of flops in series make them act like shift registers. And when SE in HIGH you can apply the test inputs one by one . In our design (FIGURE 1) the gate (Circled) has to be tested now. For this we have to apply both inputs to the AND gate as high and check if the output is HIGH . If its high than we can say that the Gate is fault free or else its faulty.Follow  the steps below to apply the test inputs to this gate and capture the response of this gate and verify your design.

Step 1: Make SE high (Now the scan cells act like shift registers)

Step 2:Apply test inputs to SI=1 and apply one clock. (this sets the output of first scan cell (X1 in figure 1) to 1.

Step 3: Apply SI=0. and apply one clock cycle .(this shifts output of X1 to X2 and sets output of X1 to 0).

Step 4: Apply SI=1. and apply one clock cycle.(this shifts output of X1 to X2 and output of X2 to X3 and output of X1 to 0)

Now if you observe that after step 4 we have actually set the outputs of scan cell X1 X2 and X3 to 1 , 0 and 1 respectively. 

                               

And indirectly we have applied 1 and 1 at the input to out AND gate :-) which we could not do before for any internal gates. The step after applying test input(11) to the Gate under consideration we have to check the Gates response now. Follow the steps below to capture the response of the gate.

Step 5: Make SE=0(normal mode) with primary inputs.

Step 6: Apply once clock cycle (this will make the scan cell X2 capture the response of our AND gate )

Step 7: Make SE=1(scan mode) apply one clock cycle (the caputured response of gate in X2 will we available at scan out. If the Gate is faulty the response will be 0 else it will be one.

The Simulation results for testing the AND gate is given below.

Advantages of Scan Cell 

•  We can test sequential circuits 
• Increases the control ability and make the circuit internal nodes more observable 

The Circuits are simulated using ISE and designed using Verilog

Have a look at this new course. 

Link for the coupons : Here

Barrel Shifter design using 2:1 Mux Using Verilog

RTL SCHEMATIC

SIMULATION RESULTS 

CODE

    

 To Download:Click On the PDF and press (CNTRL+S)

BLOCK USED FOR IMPLEMENTATION 

EXPLANATION :

          Barrel sifter which are triggered using clock operate sequentially. For a shift or rotate of  N bits you will have to apply N clock cycles. Mux can be used to make the shift/rotate operation faster by converting the sequential circuit to computational logic. Just by application of a single clock cycle N shift/rotate can be done. The circuit used for implementation above is a simple configuration for rotate right operation. If you want to customize the design for shift(right/left) or rotate(R/L) the select line connection has to be changed accordingly. Also have a look at our exciting new course for free

Link for the coupons : Here 

Carry select Adder using Verilog

                                                           RTL SCHEMATIC





















                                                 

SIMULATION RESULTS

                                                                   CODE



 To Download:Click On the PDF and press (CNTRL+S)

BLOCK DIAGRAM FOR IMPLEMENTATION 

Advantages : 

• No need to wait for carry in every stage
• Once the carry is known immediately the result can be obtained
• Low delay of just 3 Ripple Carry Adders

I have been getting lot of mail & requests to provide the test bench also for CSA. Here is the Test feature module for CSA for you :


module test_csa;

// Inputs
reg [3:0] a;
reg [3:0] b;
reg cin;

// Outputs
wire [3:0] sum;
wire co;

// Instantiate the Unit Under Test (UUT)
carry_select uut (
.a(a), 
.b(b), 
.cin(cin), 
.sum(sum), 
.co(co)
);

initial begin
// Initialize Inputs
a = 0;
b = 0;
cin = 0;
#100;

a = 4'd5;
b = 4'd10;
cin = 0;
#100;

a = 4'd5;
b = 4'd10;
cin = 1;
#100;


a = 4'd15;
b = 4'd10;
cin = 0;
#100;


a = 4'd15;
b = 4'd11;
cin = 1;
#100;


// Add stimulus here

end

endmodule

Also look at our exciting new course

Link for the coupons : Here

Discrete cosine transform using verilog (DCT)

module dct1(sel,y);

  input [2:0]sel;

  output reg [15:0]y; 

  wire [15:0]y0,y1,y2,y3,y4,y5,y6,y7;

  wire [7:0]p0,p1,p2,p3,p10,p11,p100,m0,m1,m2,m3,m10,m11,m100;

  wire [15:0]n0,n1,n2,n3,q0,q1,q2,q3;

  wire [7:0]x0,x1,x2,x3,x4,x5,x6,x7;

// pre declared

parameter c1=8'b11111011;

parameter c2=8'b11101100;

parameter c3=8'b11010100;

parameter c4=8'b10110101;

parameter c5=8'b10001110;

parameter c6=8'b01100001;

parameter c7=8'b00110001;

// pre declared

assign x0=8'b10110;

assign x1=8'b1001;

assign x2=8'b101;

assign x3=8'b1111;

assign x4=8'b1011;

assign x5=8'b10;

assign x6=8'b100;

assign x7=8'b10010;

//Butter Fly Stages

//stage1

bfly1 s11(x0,x7,p0,m0);

bfly1 s12(x3,x4,p1,m1);

bfly1 s13(x1,x6,p2,m2); 

bfly1 s14(x2,x5,p3,m3);

//stage2

bfly2 s21(m0,m1,c1,c7,n0,q0); 

bfly2 s22(m2,m3,c3,c5,n1,q1);

bfly2 s23(m0,m1,c5,c3,n2,q2);

bfly2 s24(m2,m3,c7,c1,n3,q3);

bfly1 s15(p0,p1,p10,m10);

bfly1 s16(p2,p3,p11,m11);

//stage3

bfly2 s31(m10,m11,c2,c6,y2,y6);

bfly1 s32(p10,p11,p100,m100);

assign y1=n0+n1;

assign y7=q0+(~q1+1);

assign y5=n2+(~q3+1);

assign y3=q2+(~n3+1);

assign y0=p100*c4;

assign y4=m100*c4;

always@(sel)

case(sel)

  0:begin y=y0; end

  1:begin y=y1; end

  2:begin y=y2; end

  3:begin y=y3; end

  4:begin y=y4; end

  5:begin y=y5; end

  6:begin y=y6; end

  7:begin y=y7; end

endcase

 endmodule

module bfly1(x,y,p,m);

  input [7:0]x,y;

  output[7:0]p,m;

  assign p=x+y;

  assign m=x+(~y+1);

  endmodule

module bfly2(x,y,cx,cy,sx,sy);

  input [7:0]x,y,cx,cy;

  output [15:0]sx,sy;

   assign sx=(x*cx)+(y*cy);

  assign sy=(x*cy)+(~(y*cx)+1);

endmodule

Link for the coupons : Here

THE ABOVE DESIGN IS FOR 8 POINT DCT

Types pf flip flops with Verilog code

Flip flop are basic storage elements and the soul for sequential circuit design. Based on the application & the need we can design and use a flip flop. Few of the flip flops which are usually used for sequential circuits and for memory design are

You can code for any given FF with the truth table and thereby converting them into a logic gate configuration which is quite a simple task as far as these flip flops are concerned.

• SR FF
• JK FF
• D FF
• T- FF

*********************************************************************************

SR-FF

     Characteristic equation: Q(next) = S + R'Q ,SR = 0

S	R	Q(next)
0	0	Q
0	1	0
1	0	1
1	1	undefined

From the truth table its clear that the FF has two inputs. S & R represents Set & Reset respectively. To model this FF we can use the CASE statement and define all the four input combination and the related output .Its always a good design to have a reset for your FF so as to bring it to a defined stage at any point of time asynchronously. If your design requires the use of output and its compliment then it can also be defined in your code as follows:

Verilog code for SR Flip-Flop

module srff(s,r,clk,rst, q,qb);

    input s,r,clk,rst;

    output q,qb;

               reg q,qb; 

              reg [1:0]sr;

             always@(posedge clk,posedge rst)

            begin

             sr={s,r}; //concatenate S&R to a 2 bit value

             if(rst==0) // when reset is not asserted

                        begin

                        case (sr)

                        2'd1:q=1'b0;

                        2'd2:q=1'b1;

                        2'd3:q=1'b1;

                        default: begin end

                        endcase

                        end

            else                              // when reset is asserted 

            begin

                        q=1'b0;

                        end

                       

                        qb=~q;

                        end

 endmodule

 In the above design you must have noticed that the input combination "11" is also defined which is not true in case of SR FF as its a undetermined state. To correct the design u can model the same using gate level coding using NAND or NOR gates as shown using the inbuilt function   nand(); available in the library.

*********************************************************************************

*********************************************************************************

J-K FF

     Q(next) = JQ' + K'Q

J	K	Q(next)
0	0	Q
0	1	0
1	0	1
1	1	Q'(toggle)

 This one is similar to the SR FF except that the "11" state defines a state where the output toggles between 1 & 0.  The same design for SR can be extended with two more nand gates to define the JK.

Verilog code for JK Flip Flop

`define TICK #2 //Flip-flop time delay 2 units

module jkflop(j,k,clk,rst,q);

input j,k,clk,rst;

output q;

reg q;

always @(posedge clk)begin

if(j==1 & k==1 & rst==0)begin

q =`TICK ~q; //Toggles

end

else if(j==1 & k==0 & rst==0)begin

q = `TICK 1; //Set

end

else if(j==0 & k==1)begin

q = `TICK 0; //Cleared

end

end

always @(posedge rst)begin

q = 0; //The reset normally has negligible delay and hence ignored.

end

 endmodule

The above code defines the time delay also for the FF.

********************************************************************************* 

Link for the coupons : Here

********************************************************************************* 

D-FF

                            Q(next) = D 

D	Q(next)
0	0
1	1

This one is the simplest of all the FF and also easy to model . Though its the simplest one its the most used FF for designs.

Verilog Code for D-Flip Flop

// code for dff

module Dff(input d,input clk,output reg q);

  always @(posedge clk) // note: lines whithin the always block are executed sequententialy 

  begin

  q=d;

  end 

endmodule

// code ends

 *********************************************************************************

 *********************************************************************************

T-FF

                              Q(next) = TQ' + T'Q

T	Q(next)
0	Q
1	Q'

 This one is the next simplest FF after D. Here the output is  retains the previous state when input is 0. And when the input is 1 the output toggles i.e for every rising edge of the clock when input is 1 the output toggles from its previous value.

Verilog code for T flip flop

module tff_sync_reset (

data  , // Data Input

clk   , // Clock Input

reset , // Reset input

q       // Q output

);

input data, clk, reset ;

output q;

reg q;

always @ ( posedge clk)

if (~reset) begin

  q <= 1'b0;

end else if (data) begin

  q <= !q;

end

*********************************************************************************